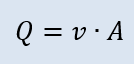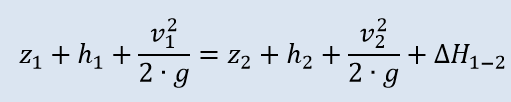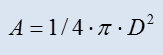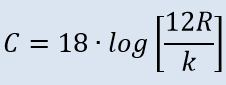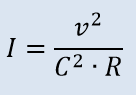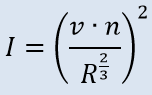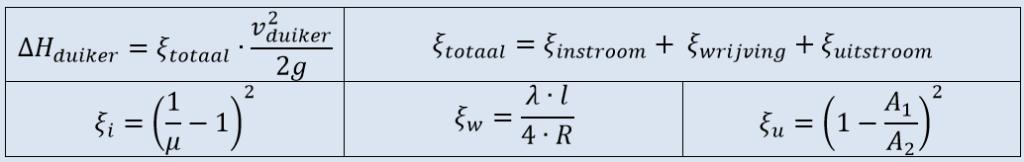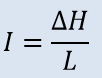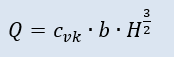General assumptions
- Flow is turbulent.
So formulas of Manning, Chezy and Darcy-Weisbach can be used. - Flow is sub-critical.
So calculations of water-levels start downstream and goes upstream. At weirs super-critical flow may occur. - Flow is steady
Discharge is not changing rapidly. Of-course over time discharge (and thus water-levels etc) can change. - Sea is salt water, on the island fresh water
- There are two main watersystems. The watersystem on the island and the sea (waves, tide, current). The connection between the two are by the culvert in the dike and seepage. High tide in combination with low water level on the island could make water flow from sea to the island. High tide can cause seepage to the land, low tide seepage to sea. Maybe in high tide in combination with big waves can cause water flowing over the dike to the island.
- Water enters the systeem by: rainfall and seepage.
- Water leaves the island through : Culvert in dike, pumping station, seepage and evapotranspiration.
- System is dendritic.
So water has one direction to flow.
Calculations in FD_watersystems
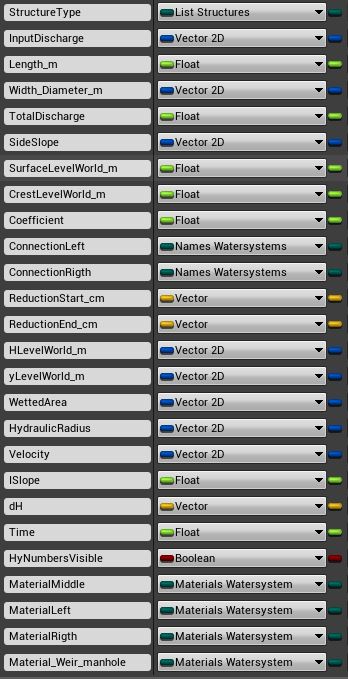
- For each branch waterlevel (ylevel) and Energylevel (Hlevel) are calculated at the beginning (.x) and end (.y) of the branch. This info is stored in WatersystemData.
- Hlevel.x = Hlevel.y downstream branch.
- yLevel.x = yLevel.y downstream branch. Consequence of this strategy is that when there is a significant change in dimension or discharge, a short branche is needed. In this short branch the transfer between the 2 different velocityheads takes place. With change in discharge this short branch is located downstream, with change in dimension this short branch is located upstream
- Weir is an exception. Hlevel.x is calculated based on the crestlevel.
- Over the length of a branch, the basic dimensions are the same, only the surfacelevel at x and y may differ. Exception is the connector, you have different width and slope downstream and upstream!!
- CulvertRectangle: If downstreams waterdepth < Height culvert : Type is converted to Trapezium. Note: With high velocities, water level will rise and the type maybe should be concerted back to culvertrectangle. This can be solved by splitting het culvert in several branches.
- In a branch (between 2 points) discharge is always the same.
- 2 special branches when calculating. First is the outflow: Discharge = 0. Value in InputDischarge.x is the velocity in the receiving water. Second is the weir : There is a jump in HlevelWorld compared to the downstream waterlevel.
- Weir is always assumed as free flow. And as a short crest. Waterlevel .x and .y are the same.
- Based on ylevel.x. Slope Hline is calculated. Hlevel.y is calculated.
Workflow calculation
In the case of type = trapezium
- HlevelWorld_m.x = HlevelWorld.y previous branch
- yLevelWorld_m.x = yLevelWorld.y previous branch
- Get Discharge from point upstreams
- Calculate Depth_m.x ,WettedArea.x, WetterPerimeter.x, HydraulicRadius.x, Velocity.x
- Calculate Hslope, dH, Time
- HlevelWorld_m.y = HlevelWord_m.x + dH
ylevelWorld_m.y = yLevelWorld,x + dH - Calculate Depth_m.y ,WettedArea.y, Velocity.y, VelocityHead
ylevelWorld_m.y= HLevelWorld_m.y – VelocityHead
- Outflow down-streams is calculated separate
- Check if branch is weir. If weir calculate H above weir, convert to HlevelWorld_m.x = HlevelWorld.y. yLevelWorld_m = CrestlevelLevelWorld_m + 2/3 * H.
- If branch is not weir
- If branch = connector; calculate average width and average slope
- Calculate Depth_m.x ,WettedArea.x, WetterPerimeter.x, HydraulicRadius.x, Velocity.x
- Calculate Hslope, dH, Time
- HlevelWorld_m.y = HlevelWord_m.x + dH
- ylevelWorld_m.y = yLevelWorld,x + dH
- Calculate Depth_m.y ,WettedArea.y, Velocity.y, VelocityHead
- ylevelWorld_m.y= HLevelWorld_m.y – VelocityHead
Culvert and Rectangle Culvert
- dH is a 3d vector. x = dH outflow, y dH friction, z dH inflow
- dH x outflow based on carnot
- dH y friction based on Chezy, with coeff = k (m)
- dH z inflow based on contraction coefficient of 0,6, so xi = 0,44
- If branch downstream = culvert, dH x = 0
- If branch upstream = culvert dH z = 0
- Extra info needed is type up-streams and down streams. local_type_up and local_type_down
- Extra info needed is W and H up and down if type is culvert. local_WH_up and local_WH_down
- Hlevel.x culvert = Hlevel.y type_down + dH.x
- Hlevel.y culvert = Hlevel.x + dH.y. So dh.z is not added yet
- Ylevel.x and Ylevel.y are based on Hlevel.x .y – velocityhead
- dH.x and dH.z are based on the type of the adjacent branch.
- dH.x and dH.z is not yet calculated with Rectangle Culvert.
Formulas